El plano complejo

El plano complejo

• Cada número complejo $z=(x,y)=x+iy$ se puede describir en un plano por el punto con coordenadas $x,y$. En este plano complejo el eje horizontal se llama eje real y el vertical se llama eje imaginario.
• En este plano, $z$ y $\overline{z}$ son reflejados por el eje real. También $\vert z\vert$ representa la distancia al origen.
• Todo complejo distinto de cero se puede escribir como producto de un número real y un complejo de módulo uno, a saber: $z=\vert z\vert \frac{z}{\vert z\vert }$.
• Los complejos de módulo uno se dibujan en el plano complejo en la circunferencia unitaria: $\{z\in \mathbb{C}\mid \vert z\vert =1\}$.

• Si $\theta$ es un ángulo tal que $\cos\theta=\frac{x}{\vert z\vert }$ y $\sin\theta=\frac{y}{\vert z\vert }$, entonces el complejo $z\ne 0$ se escribe como:

  $$z=|z|(\cos \theta+i\sin\theta)$$

  llamada forma polar del número complejo.

Argumento de un número complejo.

Puntos en la circunferencia unitaria

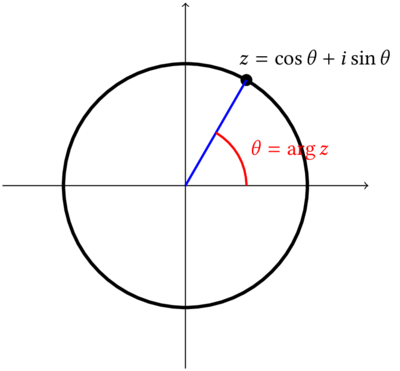
Cualquier ángulo $\theta$ que cumpla que $z=\cos\theta+i\sin\theta$ se llama argumento de $z$.

Ejemplos

Para un complejo $z\ne 0$, definimos su argumento $\arg z$ como el argumento de $\frac{z}{\vert z\vert }$.

Por ejemplo:

• $\arg i=90^{\circ}=\frac{\pi}{2}$,
• $\arg(i+1)=\frac{\pi}{4}$,
• $\arg(-1)=\pi$.
• También $3\pi$, $-\pi$, etc. son valores de $\arg(-1)$.

Propiedades del argumento

• Si $z_{1}=\cos\theta+i\sin\theta$ y $z_{2}=\cos\psi+i\sin\psi$, entonces

  $$z_{1}z_{2}=\cos(\theta+\psi)+i\sin(\theta+\psi).$$

• Por lo tanto, se obtiene la fórmula de DeMoivre:

  $$(\cos\theta+i\sin\theta)^{n}=\cos n\theta+i\sin n\theta$$

• La fórmula de DeMoivre se puede usar además para extraer raíces a números complejos.