Homología de un complejo disconexo
23 Mar 2021 La presentación en pdfConsideremos el complejo simplicial \(\Delta\) cuyo conjunto de caras maximales es \(\mathcal{F}(\Delta)=\{ab, cd, ef\}\).
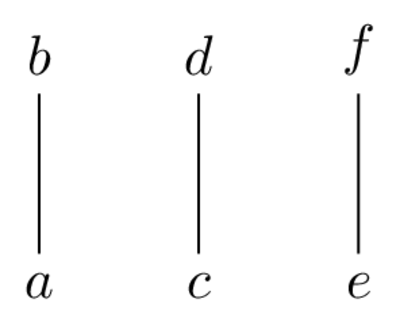
Figure 1: Ejemplo
1 Cálculo de \(H_{0}\)
Calculemos \(H_{0}(\Delta, R)=Z_{0}(\Delta,R)/B_{0}(\Delta,R)\). En este caso \(Z_{0}(\Delta,R)=\ker\partial_{0}\), donde \(\partial_{0}\colon C_{0}(\Delta,R)\to C_{-1}(\Delta,R)=R\). La matriz (respecto a las bases usuales) de \(\partial_{0}\) es \((1 1 1 1 1 1)\). Unos conjunto de generadores del espacio nulo de esta matriz es (1,-1,0,0,0,0), (1,0,-1,0,0,0), (1,0,0,-1,0,0), (1,0,0,0,-1,0), (1,0,0,0,0,-1), y esos vectores se corresponden con \(a-b, a-c, a-d, a-e, a-f\).
Consideremos \(B_{0}(\Delta,R)\), es decir, la imagen de \(\partial_{1}\colon C_{1}(\Delta,R)\to C_{0}(\Delta,R)\). Tenemos que \(H_{0}(\Delta, R)\) está generado por \(\overline{a-b}\), \(\overline{a-c}\), \(\overline{a-d}\), \(\overline{a-e}\), \(\overline{a-f}\). Como \(\partial_{1}(b\wedge a)=a-b\), tenemos que \(\overline{a-b}=0\).
Observemos que \(a-c=a-d+(d-c)=a-d + \partial_{1}(c\wedge d)\). Esto implica que \(\overline{a-c}=\overline{a-d}\). Análogamente \(\overline{a-e}=\overline{a-f}\), pues \(a-e=a-f+(f-e)=a-f+\partial_{1}(e\wedge f)\). Por lo tanto, \(H_{0}(\Delta, R)=\langle \overline{a-c}, \overline{a-e}\rangle\).
Definiciones
- Si \(z_{1},z_{2}\in Z_{n}(\Delta,R)\) son tales que \(z_{1}-z_{2}\in B_{n}(\Delta,R)\), decimos que \(z_{1},z_{2}\) son homólogos.
- Si \(R\) es un campo, a \(\dim H_{n}(\Delta,R)\) se le llama el \(n\)-ésimo número de Betti.
2 Cálculo de \(H_{1}\)
Tenemos que el complejo dado es homotópico a un complejo simplicial \(\Delta'\) que conste solo de 3 puntos aislados (es decir , que sus caras maximales sean 3 0-simplejos). Como \(H_{1}(\Delta,R)=H_{1}(\Delta',R)\), y \(C_{1}(\Delta',R)=0\), entonces \(H_{1}(\Delta,R)=0\). En general \(H_{n}(\Delta,R)=0\) para todo \(n>0\).