Homología del toro

23 Mar 2021 La presentación en pdf

Consideremos el complejo simplicial \(\Delta\).

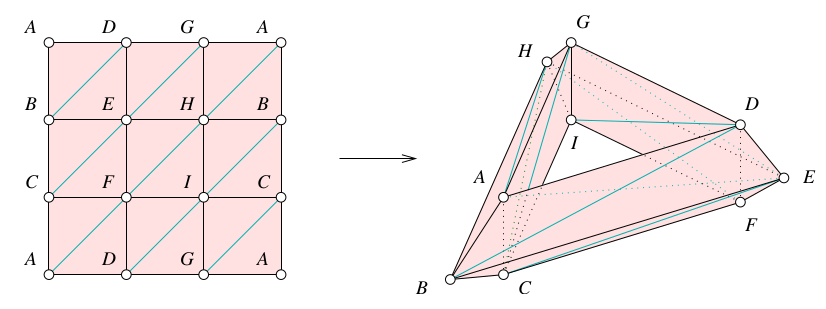
Hay 9 0-simplejos, por lo tanto \(C_{0}(\Delta,R)=\langle A,B,C,D,E,F,G,H,I\rangle\). Tenemos que \(\dim C_{1}(\Delta,R)=27\), y \(\dim C_{2}(\Delta,R)=18\).

Observemos que \(A\wedge B+B\wedge C+C\wedge A\in Z_{1}(\Delta,R)\), pues \(\partial_{1}(A\wedge B+B\wedge C+C\wedge A)=B-A+(C-B)+(A-C)=0\).

(En adelante, escribiremos las cadenas elementales sin el símbolo \(\wedge\))

También \(DE+EF+FD\in Z_{1}(\Delta,R)\).

Consideremos \(\partial_{2}(ABD+BED+BCE+CFE+AFC+ADF)\). Esto es igual a:

\begin{multline} \label{eq:1} BD - AD + AB + ED - BD + BE + CE - BE + BC\\ + FE - CE + CF + FC - AC + AF + DF - AF + AD\\ = AB + ED + BC + FE - AC + DF\\ = AB + BC + CA - DE - EF - FD \end{multline}

La diferencia del ciclo \(AB+BC+CA\) con el ciclo \(DE+EF+FD\) es entonces una frontera. Se dice que tales ciclos son homólogos. Nótese que si dos ciclos son homólogos, entonces representan la misma clase en \(H_{1}(\Delta, R)\).

Similarmente \(AD+DG+GA\in Z_{1}(\Delta, R)\). Se puede demostrar que representa una clase diferente a la de \(AB+BC+CA\) en \(H_{1}(\Delta,R)\).

Consideremos ahora \(AF+FH+HA\). Es también un ciclo, pues \(\partial_{1}(AF+FH+HA)=F-A+H-F+A-H=0\). Sin embargo, en este caso no representa una clase diferente, pues se puede demostrar que es homólogo a la suma de los dos ciclos mencionados anteriormente.