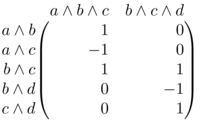Homología del plano proyectivo

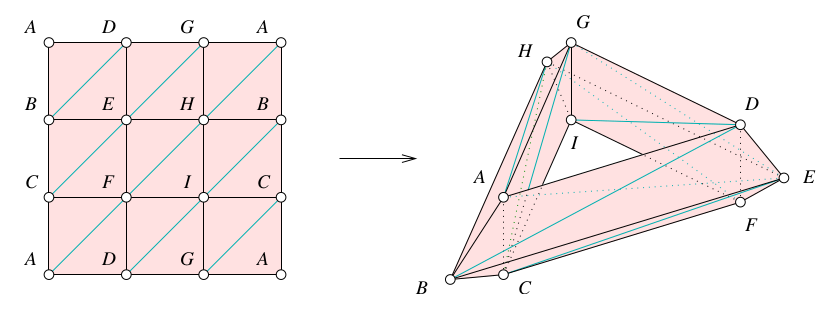
25 Mar 2021

Consideremos el siguiente complejo simplicial \(\Delta\):

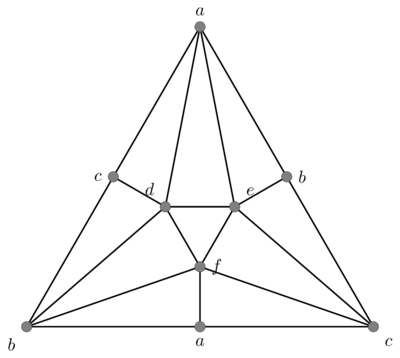
En el plano projectivo tenemos:

• 6 0-simplejos
• 15 1-simplejos
• 10 2-simplejos

En este caso, se tiene que \(z=ab+bc+ca\in Z_{1}(\Delta, R)\). Se puede demostrar que \(\overline{z}\) genera a \(H_{1}(\Delta, R)\). Pero además se tiene que \(z+z=2z\) es una frontera. Es decir, en \(H_{1}(\Delta, R)\) se tiene que \(2\overline{z}=0\). Si \(R\) es un campo de entre \(\mathbb{C}\), \(\mathbb{R}\) o \(\mathbb{Q}\), entonces se tiene que \(\overline{z}=0\) y por lo tanto \(H_{1}(\Delta,R)=0\) en ese caso. Sin embargo, si \(R=\mathbb{F}_{2}\) o si \(R=\mathbb{Z}\), no es posible dividir entre \(2\). Entonces, tenemos por ejemplo, que \(H_{1}(\Delta,\mathbb{Z})\cong \mathbb{Z}/2\mathbb{Z}\). En este caso, como el elemento \(\overline{z}\), es diferente de cero, pero tiene orden finito, se dice que es un elemento de torsión en \(H_{1}(\Delta, \mathbb{Z})\).

Homología del toro

23 Mar 2021

Consideremos el complejo simplicial \(\Delta\).

Hay 9 0-simplejos, por lo tanto \(C_{0}(\Delta,R)=\langle A,B,C,D,E,F,G,H,I\rangle\). Tenemos que \(\dim C_{1}(\Delta,R)=27\), y \(\dim C_{2}(\Delta,R)=18\).

Observemos que \(A\wedge B+B\wedge C+C\wedge A\in Z_{1}(\Delta,R)\), pues \(\partial_{1}(A\wedge B+B\wedge C+C\wedge A)=B-A+(C-B)+(A-C)=0\).

(En adelante, escribiremos las cadenas elementales sin el símbolo \(\wedge\))

También \(DE+EF+FD\in Z_{1}(\Delta,R)\).

Consideremos \(\partial_{2}(ABD+BED+BCE+CFE+AFC+ADF)\). Esto es igual a:

\begin{multline} \label{eq:1} BD - AD + AB + ED - BD + BE + CE - BE + BC\\ + FE - CE + CF + FC - AC + AF + DF - AF + AD\\ = AB + ED + BC + FE - AC + DF\\ = AB + BC + CA - DE - EF - FD \end{multline}

La diferencia del ciclo \(AB+BC+CA\) con el ciclo \(DE+EF+FD\) es entonces una frontera. Se dice que tales ciclos son homólogos. Nótese que si dos ciclos son homólogos, entonces representan la misma clase en \(H_{1}(\Delta, R)\).

Similarmente \(AD+DG+GA\in Z_{1}(\Delta, R)\). Se puede demostrar que representa una clase diferente a la de \(AB+BC+CA\) en \(H_{1}(\Delta,R)\).

Consideremos ahora \(AF+FH+HA\). Es también un ciclo, pues \(\partial_{1}(AF+FH+HA)=F-A+H-F+A-H=0\). Sin embargo, en este caso no representa una clase diferente, pues se puede demostrar que es homólogo a la suma de los dos ciclos mencionados anteriormente.

Homología de un complejo disconexo

23 Mar 2021

Consideremos el complejo simplicial \(\Delta\) cuyo conjunto de caras maximales es \(\mathcal{F}(\Delta)=\{ab, cd, ef\}\).

Más cálculos de homología

18 Mar 2021

Consideremos el complejo simplicial \(\Delta\) cuyo conjunto de caras maximales es \(\mathcal{F}(\Delta)=\{abc,bcd\}\).

Grupos abelianos

09 Mar 2021

Un grupo abeliano es un grupo donde la operación es conmutativa. Por convención, la operación en un grupo abeliano se escribe \(+\).

Si \(A\) es un grupo abeliano, podemos definir \(na\) donde \(n\in \mathbb{Z}\) y \(a\in A\), de la siguiente manera:

\begin{equation} na= \begin{cases} a+a+\cdots+a & \text{si \(n>0\)},\\ 0 & \text{si \(n=0\)},\\ -(-n)a & \text{si \(n<0\)} \end{cases} \end{equation}

(es decir, un grupo abeliano es un \(\mathbb{Z}\)-módulo).

En un grupo abeliano, cualquier subgrupo \(B\leq A\) es normal. Los elementos del grupo cociente \(A/B\) son las clases laterales de los elementos de \(A\). La clase de \(a\in A\) se puede escribir como \(a+B\) o como \(\overline{a}\).

Recordemos: \(a_{1}\sim a_{2}\) si \(a_{1}-a_{2}\in B\) define una relación de equivalencia en \(A\) donde las clases son las clases laterales.

Ejemplos:

• Sabemos que si \(A=\mathbb{Z}\), todo subgrupo de \(A\) es de la forma \(n\mathbb{Z}=\{na\mid a\in \mathbb{Z}\}\) para algún entero positivo \(n\) (puesto que todo subgrupo de un grupo cíclico es cíclico). En este caso, la relación \(a_{1}\sim a_{2}\) si y solo si \(a_{1}-a_{2}\in n\mathbb{Z}\) se traduce en que \(a_{1}\sim a_{2}\) si y solo si existe \(u\in \mathbb{Z}\) tal que \(a_{1}-a_{2}=nu\). Y esto a su vez quiere decir \(a_{1}\equiv a_{2} \mod n\) . Cada clase de equivalencia de acuerdo a ésta relación es una clase lateral, y podemos escoger a \(0,1,2,\ldots,n-1\) como representantes de las clases. Por lo tanto el grupo \(\mathbb{Z}/n\mathbb{Z}=\{\overline{0},\overline{1},\ldots,\overline{n-1}\}\).
• Si \(A,B\) son grupos abelianos, definimos \(A\oplus B=\{(a,b)\mid a\in A, b\in B\}\). La operación se define como \((a_{1},b_{1})+(a_{2},b_{2})=(a_{1}+a_{2},b_{1}+b_{2})\). Con ésta operación, se tiene un grupo abeliano.
• Consideremos el grupo abeliano \(\mathbb{Z}\oplus \mathbb{Z}=\{(a,b)\mid a,b\in \mathbb{Z}\}\). Este grupo tiene subgrupos de la forma \(m\mathbb{Z}\oplus n\mathbb{Z}\). En este caso, el cociente es \((\mathbb{Z}\oplus \mathbb{Z})/(m\mathbb{Z}\oplus n\mathbb{Z})\cong(\mathbb{Z}/m\mathbb{Z})\oplus (\mathbb{Z}/n\mathbb{Z})\). [La demostración se puede hacer usando el primer teorema de isomorfismos: Si \(f\colon A\to B\) es un morfismo de grupos suprayectivo, entonces \(A/\ker f\cong B\)].
• Consideremos el subgrupo de \(A=\mathbb{Z}\oplus \mathbb{Z}\) dado por \(B=\{(a,a)\mid a\in \mathbb{Z}\}\). En este caso, el cociente \(A/B\) se puede obtener usando el morfismo \(f\colon A\to \mathbb{Z}\) dado por \(f(a,b)=a-b\). Este morfismo es suprayectivo y su kernel es \(B\). Por lo tanto, \(A/B\cong \mathbb{Z}\) por el primer teorema de isomorfismos, donde el isomorfismo está dado por \(\overline{f}(\overline{(a,b)})=f(a,b)=a-b\). Como \(\overline{f}(\overline{(1,0)})=1\), se tiene que \(A/B=\langle \overline{(1,0)}\rangle\). Esto implica que toda clase de \(A/B\) se puede representar por un elemento de la forma \((a,0)\). Como ejercicio, encuentra el representante de la clase de \((a,b)\).

• Consideremos el subgrupo de \(A=\mathbb{Z}\oplus \mathbb{Z}\) dado por \(B=\{a(-2,2)+b(2,4)\mid a,b\in \mathbb{Z}\}\). El cociente de \(A/B\) es: \(A/B=\{\overline{(0,0)},\overline{(0,1)},\overline{(-1,3)},\overline{(1,0)},\overline{(2,0)},\overline{(3,0)},\overline{(0,3)}\}\).

  ¿ \((2,0)-(1,0)=(1,0)\in B\) ? ¿Existen \(a,b\in \mathbb{Z}\) tales que \((1,0)=a(-2,2)+b(2,4)\)?

  ¿Existen \(x,y\in \mathbb{Z}\) tales que \(\overline{(x,y)}=\overline{(0,8)}\), donde \(x,y\) sean “más sencillos”.

  Tenemos que \(\overline{(2,0)}=\overline{(0,2)}\), pues \((2,-2)\in B\).