Cálculo de homología
08 Mar 2021Consideremos el complejo simplicial \(\Delta\) cuyo conjunto de caras maximales es \(\mathcal{F}(\Delta)=\{abc,bd,cd\}\).

Figure 1: Ejemplo
1 Cálculo de \(H_{1}\).
Calculemos \(H_{1}(\Delta, R)=Z_{1}(\Delta,R)/B_{1}(\Delta,R)\). Consideremos la frontera \(\partial_{1}\colon C_{1}(\Delta,R)\to C_{0}(\Delta,R)\). En las bases dadas por las cadenas elementales, esa transformación lineal tiene matriz:
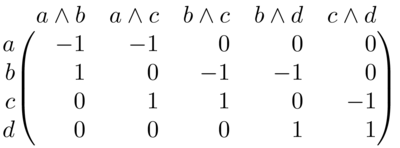
Figure 2: Matriz de \(\partial_{1}\)
El espacio nulo está generado por \((1,-1,1,0,0)^{T},(-1,1,0,-1,1)^{T}\). El primer vector se corresponde con \(a\wedge b-a\wedge c+b\wedge c\). El segundo vector se corresponde con \(-a\wedge b+a\wedge c-b\wedge d +c\wedge d\). Estos dos son generadores de \(Z_{1}(\Delta,R)\).
Este espacio nulo se puede calcular en Python con el siguiente código:
from sympy import Matrix
A=Matrix([[-1,-1, 0, 0, 0],
[ 1, 0,-1,-1, 0],
[ 0, 1, 1, 0,-1],
[ 0, 0, 0, 1, 1]])
A.nullspace()El espacio \(B_{1}(\Delta,R)\) es la imagen de la frontera \(\partial_{2}\colon C_{2}(\Delta,R)\to C_{1}(\Delta, R)\). Esta frontera tiene matriz:
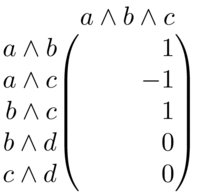
Figure 3: Matriz de \(\partial_{2}\)
Como \(\partial_{2}(a\wedge b\wedge c)=a\wedge b - a\wedge c+b\wedge c\), y éste vector es diferente de cero, genera a \(B_{1}(\Delta,R)\). Por lo tanto \(B_{1}(\Delta,R)=\langle a\wedge b - a\wedge c+b\wedge c \rangle\).
Tenemos entonces que el cociente \(Z_{1}(\Delta,R)/B_{1}(\Delta,R)\) está generado por
- \(\overline{a\wedge b-a\wedge c+b\wedge c}=\overline{0}\) y por
- \(\overline{-a\wedge b+a\wedge c-b\wedge d +c\wedge d}\).
Consideremos que \(\overline{0}=\overline{(a\wedge b-a\wedge c+b\wedge c)}\) implica \(\overline{b\wedge c}=\overline{-a\wedge b+a\wedge c}\). De ésto, se obtiene que el segundo generador es igual a \(\overline{b\wedge c-b\wedge d+c\wedge d}\). Como el primer generador es \(\overline{0}\), se obtiene que \(H_{1}(\Delta,R)\) está generado por \(\overline{b\wedge c-b\wedge d+c\wedge d}\).
2 Cálculo de \(H_{2}\)
Calculemos \(H_{2}(\Delta, R)=Z_{2}(\Delta,R)/B_{2}(\Delta,R)\). En este caso \(Z_{2}(\Delta,R)=\ker\partial_{2}=0\). Además \(B_{2}(\Delta,R)\) es la imagen de \(\partial_{3}\colon C_{3}(\Delta,R)\to C_{2}(\Delta,R)\), por lo que \(B_{2}(\Delta,R)=0\). Por lo tanto \(H_{2}(\Delta,R)=0\).
3 Cálculo de \(H_{0}\)
Calculemos \(H_{0}(\Delta, R)=Z_{0}(\Delta,R)/B_{0}(\Delta,R)\). En este caso \(Z_{0}(\Delta,R)=\ker\partial_{0}\), donde \(\partial_{0}\colon C_{0}(\Delta,R)\to C_{-1}(\Delta,R)=R\). La matriz (respecto a las bases usuales) de \(\partial_{0}\) es \((1 1 1 1)\). Un conjunto de generadores del espacio nulo de esta matriz es \(\{(1,-1,0,0), (1,0,-1,0), (1,0,0,-1)\}\), y los vectores de ese conjunto se corresponden con \(a-b, a-c, a-d\).
Calculemos \(B_{0}(\Delta,R)\), es decir, la imagen de \(\partial_{1}\colon C_{1}(\Delta,R)\to C_{0}(\Delta,R)\). Tenemos que \(\partial_{1}(b\wedge a)=a-b\), \(\partial_{1}(c\wedge a)=a-c\), \(\partial_{1}(c\wedge a+d\wedge c)=a-d\). Esto implica que \(Z_{0}(\Delta,R)=B_{0}(\Delta,R)\), por lo tanto \(H_{0}(\Delta,R)=0\).
